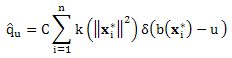Xueqing Sun
June 12th, 2011
You can distribute, remix, tweak, and build upon this work, even commercially, as long as you credit Xueqing Sun for the original creation.
I was reading a book, ‘Image Processing, Analysis, and Machine Vision, Milan Sonka, Vaclav Hlavac, Roger Boyle’ for studying mean-shift object tracking algorithm. But the book was really hard to understand, especially for a beginner of machine vision. Yesterday, with the help of Guangwei, a friend of mine (he is a scientist at National Astronomical Observatories, Chinese Academy of Science), I finally understood the algorithm. And I would like to explain what I understood for sake of helping other guys who are still struggling on this algorithm.
Heads up Questions
1. What is the probability density function of an image?
2. How does the density function contribute to target model?
3. What’s kernel function? How does it work?
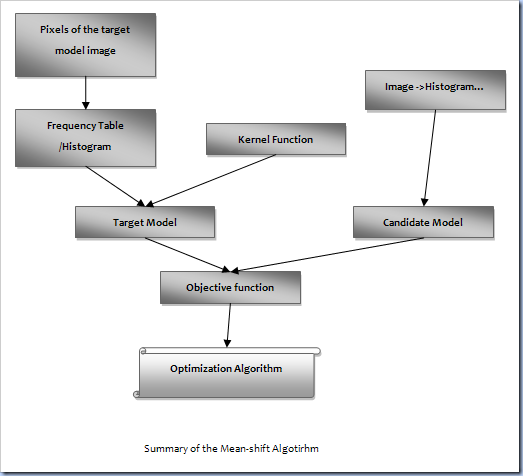
Here is the summary of the algorithm
To locate a target on an image, we must have a target model, an image which contains the target. The goal of mean-shift algorithm is to tell you the position of your target on the image. Suppose we have a target model image with 5*5 pixels. The pixel values listed below:
| x | y | pixel |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 2 | 6 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
| 1 | 0 | 0 |
| 1 | 1 | 4 |
| 1 | 2 | 7 |
| 1 | 3 | 0 |
| 1 | 4 | 4 |
| 2 | 0 | 3 |
| 2 | 1 | 5 |
| 2 | 2 | 7 |
| 2 | 3 | 1 |
| 2 | 4 | 5 |
| 3 | 0 | 7 |
| 3 | 1 | 0 |
| 3 | 2 | 9 |
| 3 | 3 | 9 |
| 3 | 4 | 2 |
| 4 | 0 | 0 |
| 4 | 1 | 1 |
| 4 | 2 | 4 |
| 4 | 3 | 3 |
| 4 | 4 | 3 |
Target model image
The row x and y are the location of a pixel on the image. And the third row ‘pixel’ is the value. For convenient purpose, we limit pixel value from 0 to 9. Now we can create a frequency table like below. Normally images are colored, but we simplified the problem from colored images to gray scale images. A colored image can be considered as a composition of three gray scale images. So the rationale explained here can be easily applied to colored images.
| bin | q |
| 1 | 8 |
| 2 | 1 |
| 3 | 3 |
| 4 | 3 |
| 5 | 3 |
| 6 | 1 |
| 7 | 4 |
| 8 | 0 |
| 9 | 2 |
Frequency
The frequency means how many pixels located in a specific bin. For example, the first row means there are 8 pixels which values are less or equal to ‘1’. Furthermore we can have histogram chart for the table.
Histogram
On the book, and many other materials, the density function of target model, defined as below:
| 1 |
The density function is closely related with the frequency table. Here the black ![]() is a vector which has m components. In this case, the m is 9 because we have 9 bins. Each component is made from corresponding bin. Let look into the component definition.
is a vector which has m components. In this case, the m is 9 because we have 9 bins. Each component is made from corresponding bin. Let look into the component definition.
| 2 |
The definition looks somewhat complex. Let’s split it into parts so we can understand it easier. First, let’s see the delta part
| 3 |
n is the pixel number. In this case we have 25 pixels. So the n is 25. ![]() is the coordinate of ith pixel in the image. For example, the first pixel coordinate is (0,0), and the second is (0,1). u means we are currently defining uth component corresponding to uth bin. Function
is the coordinate of ith pixel in the image. For example, the first pixel coordinate is (0,0), and the second is (0,1). u means we are currently defining uth component corresponding to uth bin. Function ![]() tells which bin the pixel
tells which bin the pixel ![]() go. For example, the first pixel (0,0) is 1, so it goes to bin 1, i.e.
go. For example, the first pixel (0,0) is 1, so it goes to bin 1, i.e. ![]() .
.
Actually, the formula 3 is a vector, let’s rewrite it as following:
| 4 |
The delta function gives you 1 if the pixel ![]() goes to bin u, otherwise it gives 0. So this vector works just like a mask. On the mask there are ‘1’s mark the pixels go to bin u. For example, if our image is 4*4, we might get a D vector like this:
goes to bin u, otherwise it gives 0. So this vector works just like a mask. On the mask there are ‘1’s mark the pixels go to bin u. For example, if our image is 4*4, we might get a D vector like this:
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 |
The image is a matrix. D is a vector. Just put each row of the matrix to one row in sequence then we’ll get D.
IMPORTANT
What’s the relationship between D and the frequency table? The answer is for each u,
. Actually we can form feature space only based on D, because D already represents the image in statistics way. So mean-shift algorithm is so called an algorithm that based on probability density function. But marginal pixels are unstable, so the kernel function which is a weight function does the work. It give marginal pixels less weight to make the objective function in optimization process more stable.
OK, let’s see another part of formula 2. It’s
| 5 |
Again it’s a vector. Function k is the kernel function which actually is a weight function giving each pixel position a weight. So ![]() can be defined as below:
can be defined as below:
| 6 |
It looks beautiful. I really hate ![]() which makes formula unreadable.
which makes formula unreadable.
OK, now we get the density function of target model image. The candidate density function is pretty similar.
| 7 | |
| 8 |
Formula 8 is easier to understand because we’ve already understood formula 2. The k function in formula 8 is just a transformed version of original k.
I think I’ve solved the hardest part of the mean-shift algorithm. And the rest of it would be much easier to understand because it is just kind of an optimism algorithm to find the y.